"La Geometría es el conocimiento de lo eternamente existente"Pitágoras
Pitágoras
Isla de Samos, Grecia, c. 569/570 a. C.-Metaponto, Italia, c. 475/495 a. C.
Pitágoras, el primer matemático puro de la historia, fue un filósofo y matemático griego reconocido por el Teorema de Pitágoras, el cual sigue siendo enseñado en las escuelas tras varios siglos después de haber sido formulado.
¿Quién fue Pitágoras?
La verdad es que las fuentes confiables sobre su vida son realmente escasas. Muchos de sus seguidores se encargaron de escribir datos de su maestro que parecen ensalzarlo más que retratarlo fielmente.
Probablemente nació en la isla de Samos, cerca de las costas turcas, por lo que “Pitágoras de Samos” era el nombre con el que a menudo la gente se refería a él y provenía de su ciudad natal, no de su apellido. Durante su juventud viajó a través del Mediterráneo y a Persia; conoció además a Tales de Mileto, quien le aconsejó viajar a Egipto.
Algunos seguidores afirmaron que en Samos era muy solicitado y cumplía varios cargos públicos. Cerca del año 530 a. C. viajó a la ciudad de Crotona, situada en el sur de Italia, y fijó ahí su residencia. Según algunas fuentes conoció ahí a una mujer llamada Teano, con la cual se casó y tuvo varios hijos.
Tiempo después comenzó a enseñar en Crotona y poco a poco la cantidad de seguidores se acrecentó, influidos por la elocuencia con la que se expresaba acerca de sus pensamientos. Así la cosas, fundó en la ciudad una escuela que atrajo multitud de seguidores.
Los seguidores de Pitágoras adquirieron el nombre de pitagóricos, y la escuela se convirtió en un grupo estructurado en una filosofía matemática con base en el estudio y el ejercicio. Pero los pitagóricos no eran solamente estudiantes. Disciplinados y organizados, seguían una serie de preceptos con el fin de perfeccionar su cuerpo físico y alcanzar la inmortalidad. Para eliminar toda impureza del cuerpo, se abstenían de consumir carne y frijoles, no recoger lo que había caído, etcétera. Se cree que aunque mantenían las creencias politeístas típicas de la Grecia Antigua, creían también en un ser superior a todas las divinidades.
Los ejemplos más claros de lo anterior están conformados por descubrimientos y elementos matemáticos, como el famoso Teorema de Pitágoras, adjudicado a su persona desde el siglo IV después de Cristo. De acuerdo con este teorema, el valor del cuadrado de la hipotenusa de un triángulo es igual a la suma de los cuadrados de los catetos, es decir: a2 + b2 = c2. Es una de las operaciones básicas que todo escolar aprende durante sus años de formación elemental. No obstante, los babilonios y los habitantes de la India ya tenían este conocimiento.
También se le atribuye la creación de la Tetraktys, un triángulo compuesto por 10 puntos alineados en 4 filas que constituyó un símbolo místico para los pitagóricos, y la teoría de que los planetas y las estrellas se movían de acuerdo con ecuaciones matemáticas que correspondían a notas musicales, produciéndose así las sinfonías. Esto es conocido como “armonía de las esferas”. De hecho, para Pitágoras y sus seguidores las cosas eran básicamente números.
Al parecer, en el 500 a. C. se suscitó en Crotona un levantamiento en contra de los pitagóricos, probablemente motivada por juegos de poderes. Pitágoras huyó entonces y lo que sucedió con él es inexacto; pudo haber sido asesinado o haber muerto un tiempo después.
La influencia de Pitágoras en la filosofía probablemente trastocó la existencia de pensadores posteriores como Platón y Aristóteles.
¿Qué es el Teorema de Pitágoras?
Debemos tomar en cuenta que esta ley solo se cumple para un tipo de triángulo muy particular, el triángulo rectángulo, que es aquel donde dos de los tres lados, que son los denominados catetos, forman un ángulo recto, es decir, que mide 90º.
El teorema de Pitágoras lo observamos en la siguiente fórmula, donde AB y BC son los catetos y AC es la hipotenusa del triángulo que mostramos en el gráfico de abajo.
AB2+BC2=AC2
Entonces, el teorema de Pitágoras nos permite calcular la longitud de uno de los lados del triángulo cuando conocemos los otros dos. Asimismo, sabiendo la longitud de todos los lados, podemos verificar sin un triángulo es rectángulo.
Cabe señalar que en la figura mostrada las medidas de los ángulos son referenciales. Pueden tener distintas medidas, pero en todos los triángulos, en general (no solo en los rectángulos), los ángulos interiores siempre deben sumar 180º. Por ende, si uno mide 90º, la suma de los otros dos necesariamente debe ser 90º.
Entonces, tomando en cuenta lo anterior, en un triángulo rectángulo uno de los ángulos es recto y los otros dos deben ser agudos (menores que 90º).
Aplicación del Teorema de Pitágoras (Ejemplo)
Supongamos que tenemos un triángulo rectángulo, siendo la longitud de su hipotenusa 15 metros y la de uno de sus catetos, 10 metros ¿Cuánto mide el otro cateto?
Entonces, desarrollamos la operación:
152=102+x2
225=100+x2
x2=125
x=11,1803 metros
Veamos otro ejercicio. Nos podrían decir que se tiene un triángulo cuyos lados miden 8, 11 y 14 metros. ¿Puede ser un triángulo rectángulo?
82+112=64+121=185
142=196
185 ≠ 196
Por lo tanto, el triángulo no puede ser rectángulo (en este punto cabe destacar que la hipotenusa siempre medirá más que los catetos).
Ahora, como tercer ejemplo de aplicación de este teorema, supongamos que nos dicen que tenemos un cuadrado cuyos lados miden 12 metros. ¿Cuál es la longitud de su diagonal?
En este caso, debemos recordar que los ángulos interiores de un cuadrado miden 90º. Por lo tanto, cuando trazamos una diagonal dividimos la figura en dos triángulos rectángulos (como se observa en la figura inferior).
Entonces, la longitud de la diagonal (x) sería:
122 + 122 = x2
144 + 144 = x2
x2 = 288
x = 16,9706 metros
Otros Ejemplos:
1. Calcular la hipotenusa del triángulo rectángulo de lados 3cm y 4cm.
Solución:
Los lados son
Aplicando el teorema de Pitágoras,
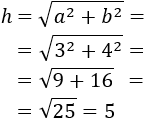
Por tanto, la hipotenusa mide 5cm.
2. Calcular la altura del siguiente triángulo sabiendo que sus lados miden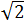 
, 
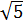y su base 3
Solución:
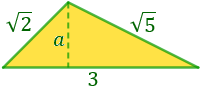
Para poder calcular la altura del triángulo, a, tenemos que dividirlo en dos triángulos rectángulos (para poder aplicar el teorema de Pitágoras).
Los dos triángulos son los siguientes:
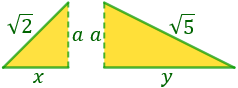
La base del triángulo (que mide 3) se divide en dos (la base de cada triángulo). No sabemos cuánto mide cada base, pero sí que sabemos que
Aplicamos Pitágoras al primer triángulo y obtenemos la ecuación:
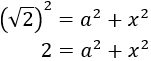
Notemos que no conocemos ninguno de los dos catetos.
Procediendo del mismo modo para el otro triángulo, obtenemos
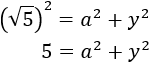
Es decir, tenemos las siguientes ecuaciones:
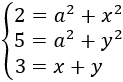
Podemos aislar la y en la tercera ecuación, obteniendo
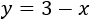
En la segunda ecuación tenemos una y, que sabemos que es 3 - x, así que sustituimos en ella:
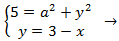
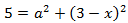
Como tenemos una resta al cuadrado, aplicamos la fórmula del binomio de Newton, que recordamos que es
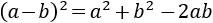
Por tanto,
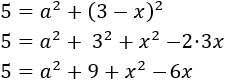
Ahora despejamos a 2
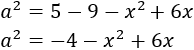
Recordemos que también teníamos la ecuación
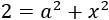
Despejamos también en ella a 2
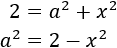
Es decir, las dos ecuaciones que tenemos son
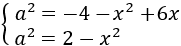
Y como a 2 = a 2, podemos igualar ambas expresiones obteniendo una ecuación de primer grado
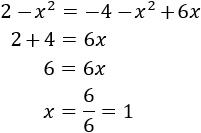
Sabiendo el valor de x podemos obtener el de y
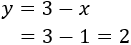
Ya sabemos cuánto mide cada base y podemos ahora calcular la altura.
La primera de las ecuaciones era
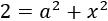
Como sabemos que x = 1 tenemos que
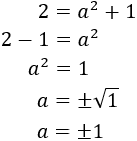
Y como es la altura, no puede ser negativa. Por tanto, la altura del triángulo es
3. Calcular la altura que podemos alcanzar con una escalera de 3 metros apoyada sobre la pared si la parte inferior la situamos a 70 centímetros de ésta.
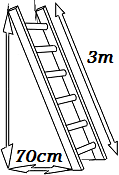
Solución:
Hay que tener en cuenta que las unidades de medida no son las mismas. Podemos escribirlas todas en metros, así que
70 cm = 7 dm = 0.7 m
El triángulo que tenemos es
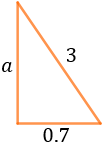
La altura es uno de los catetos. Aplicamos el teorema de Pitágoras para calcularla:
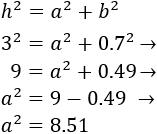
Por tanto,
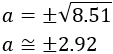
Pero como es la altura, debe ser positiva. Por tanto, la altura será, aproximadamente
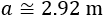
Aprende con videos:
Metodo de Polya:
1. Paso 1: Entender el problema
2. Paso 2: Configurar un plan
3. Paso 3: Ejecutar el plan
4. Paso 4: Mirar hacia atrás
Comentarios
Publicar un comentario